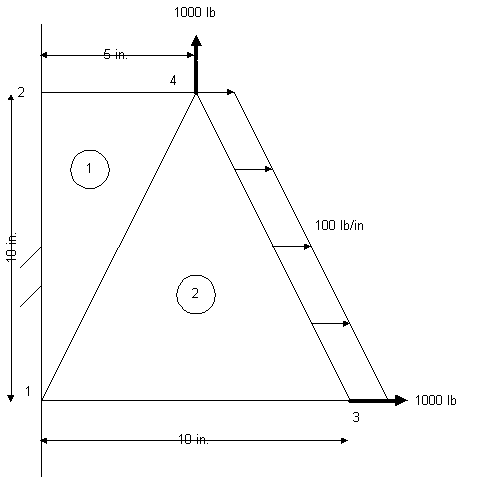
Example on FEM constant strain triangular element

thickness

enter the nodal coordinates

element 1: nodes: 1,2,4

element 2: nodes: 1,3,4

area of element 1

area of element 2

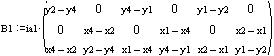
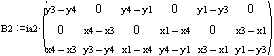
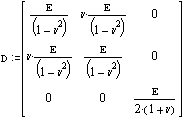
Create stiffness matrices

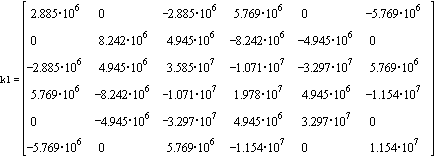
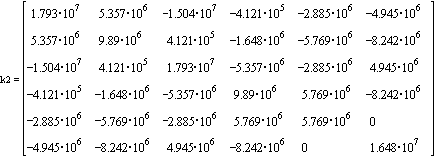
Expand stiffness matrices

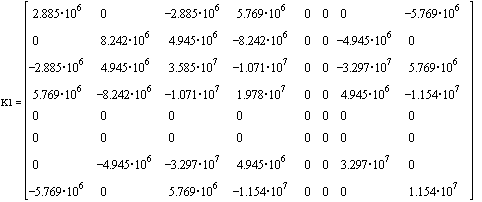
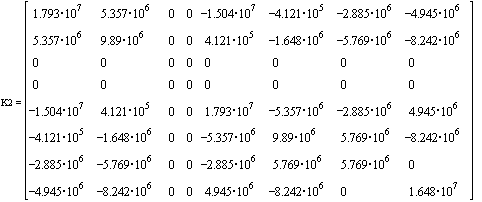
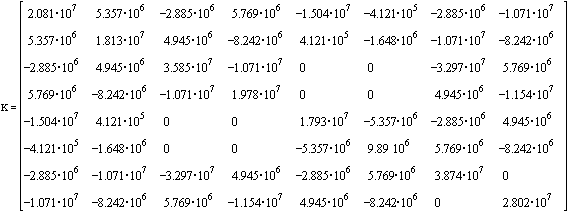
Reduced Stiffness matrix

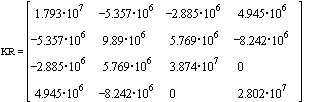
Boundary Conditions:

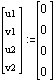
Forces: Two forces on nodes 3 and 4 in x and y directions respectively. Distribted force on 3-4 endge (element 2 only).

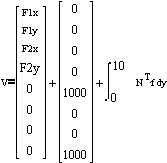
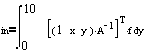
The line equation is,

A matrix is,

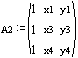
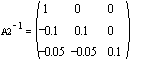
Multiply by the equation of the 3-4 edge

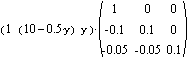
results in,

by matrix transposition, yields

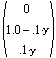
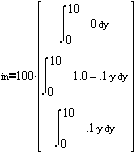
yields

Force correspond to u1,u3, and u4 respectively

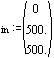
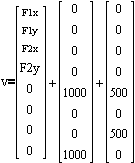
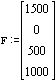
displacements of nodes 3 and 4 in x and y directions

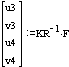
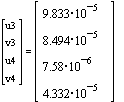
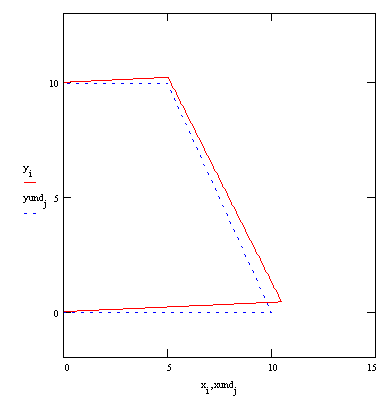
Display the results:

magnification factor

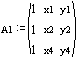
Upper edge:

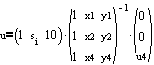
yields

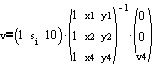
yields

Outer edge:

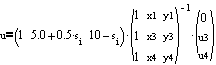
yields

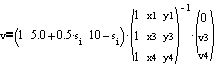
yields

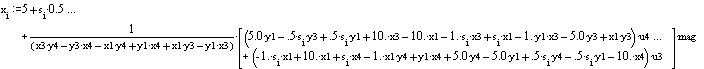
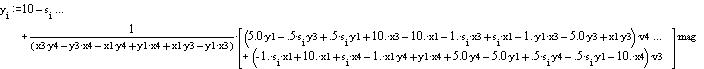
Lower edge

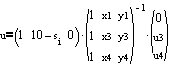
yields

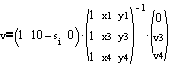
yields

Undeformed shape